Publications | Pantelis R. Vlachas

2025

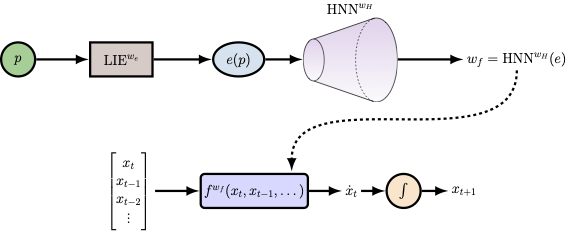Beyond Static Models: Hypernetworks for Adaptive and Generalizable Forecasting in Complex Parametric Dynamical Systems

Pantelis R. Vlachas, Konstantinos Vlachas, and Eleni Chatzi

2025

Abs arXiv Bib HTML PDF

Dynamical systems play a key role in modeling, forecasting, and decision-making across a wide range of scientific domains. However, variations in system parameters, also referred to as parametric variability, can lead to drastically different model behavior and output, posing challenges for constructing models that generalize across parameter regimes. In this work, we introduce the Parametric Hypernetwork for Learning Interpolated Networks (PHLieNet), a framework that simultaneously learns: (a) a global mapping from the parameter space to a nonlinear embedding and (b) a mapping from the inferred embedding to the weights of a dynamics propagation network. The learned embedding serves as a latent representation that modulates a base network, termed the hypernetwork, enabling it to generate the weights of a target network responsible for forecasting the system’s state evolution conditioned on the previous time history. By interpolating in the space of models rather than observations, PHLieNet facilitates smooth transitions across parameterized system behaviors, enabling a unified model that captures the dynamic behavior across a broad range of system parameterizations. The performance of the proposed technique is validated in a series of dynamical systems with respect to its ability to extrapolate in time and interpolate and extrapolate in the parameter space, i.e., generalize to dynamics that were unseen during training. In all cases, our approach outperforms or matches state-of-the-art baselines in both short-term forecast accuracy and in capturing long-term dynamical features, such as attractor statistics.
@article{vlachas2025beyond, title = {Beyond Static Models: Hypernetworks for Adaptive and Generalizable Forecasting in Complex Parametric Dynamical Systems}, author = {Vlachas, Pantelis R. and Vlachas, Konstantinos and Chatzi, Eleni}, year = {2025} }

2024

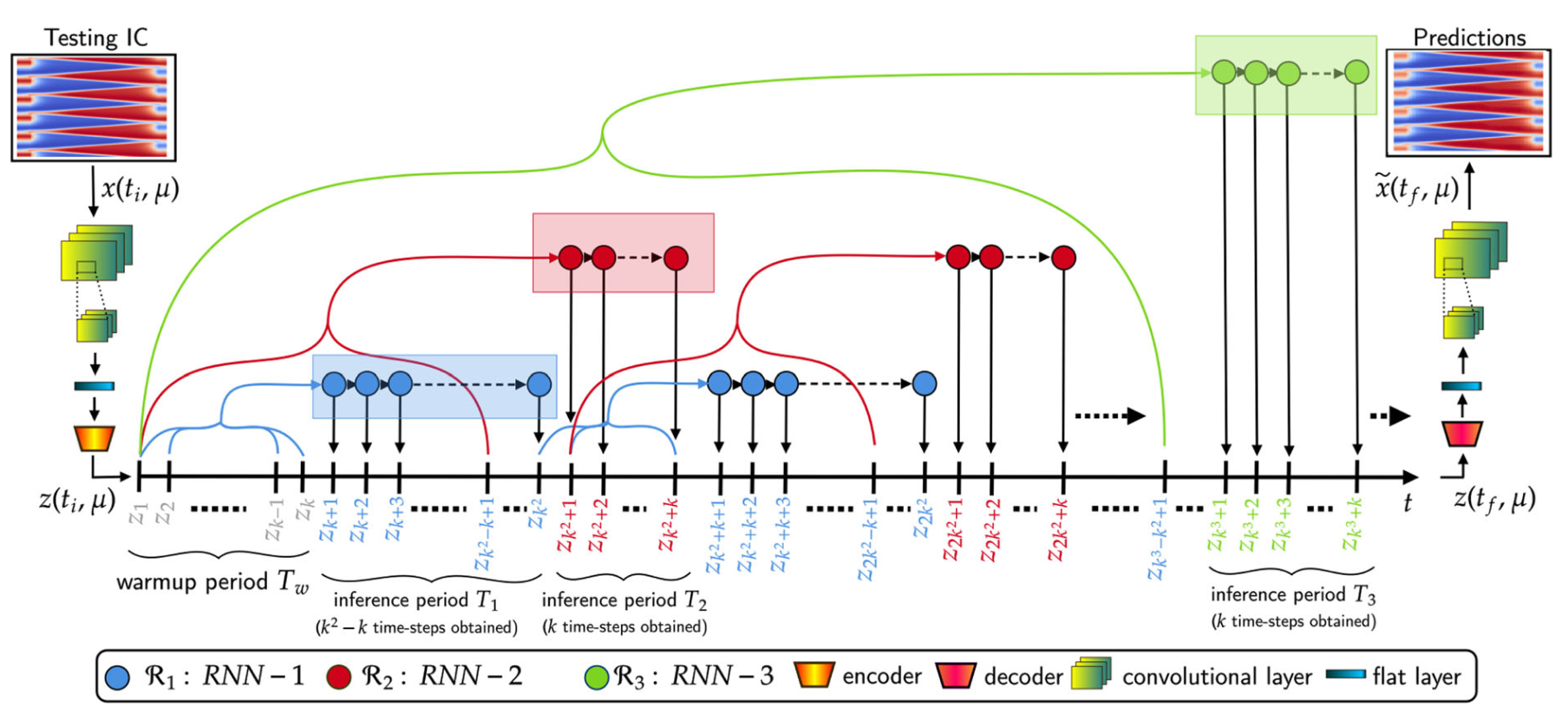RefreshNet: learning multiscale dynamics through hierarchical refreshing

Junaid Farooq, Danish Rafiq, Pantelis R. Vlachas, and Mohammad Abid Bazaz

Nonlinear Dynamics, 2024

Abs Bib PDF

Forecasting complex system dynamics, particularly for long-term predictions, is persistently hindered by error accumulation and computational burdens. This study presents RefreshNet, a multiscale framework developed to overcome these challenges, delivering an unprecedented balance between computational efficiency and predictive accuracy. RefreshNet incorporates convolutional autoencoders to identify a reduced order latent space capturing essential features of the dynamics, and strategically employs multiple recurrent neural network blocks operating at varying temporal resolutions within the latent space, thus allowing the capture of latent dynamics at multiple temporal scales. The unique “refreshing” mechanism in RefreshNet allows coarser blocks to reset inputs of finer blocks, effectively controlling and alleviating error accumulation. This design demonstrates superiority over existing techniques regarding computational efficiency and predictive accuracy, especially in long-term forecasting. The framework is validated using three benchmark applications: the FitzHugh–Nagumo system, the Reaction–Diffusion equation, and Kuramoto–Sivashinsky dynamics. RefreshNet significantly outperforms state-of-the-art methods in long-term forecasting accuracy and speed, marking a significant advancement in modeling complex systems and opening new avenues in understanding and predicting their behavior.
@article{farooq2024refreshnet, title = {RefreshNet: learning multiscale dynamics through hierarchical refreshing}, author = {Farooq, Junaid and Rafiq, Danish and Vlachas, Pantelis R. and Bazaz, Mohammad Abid}, journal = {Nonlinear Dynamics}, year = {2024}, volume = {112}, pages = {14479--14496}, doi = {10.1007/s11071-024-09813-3}, }
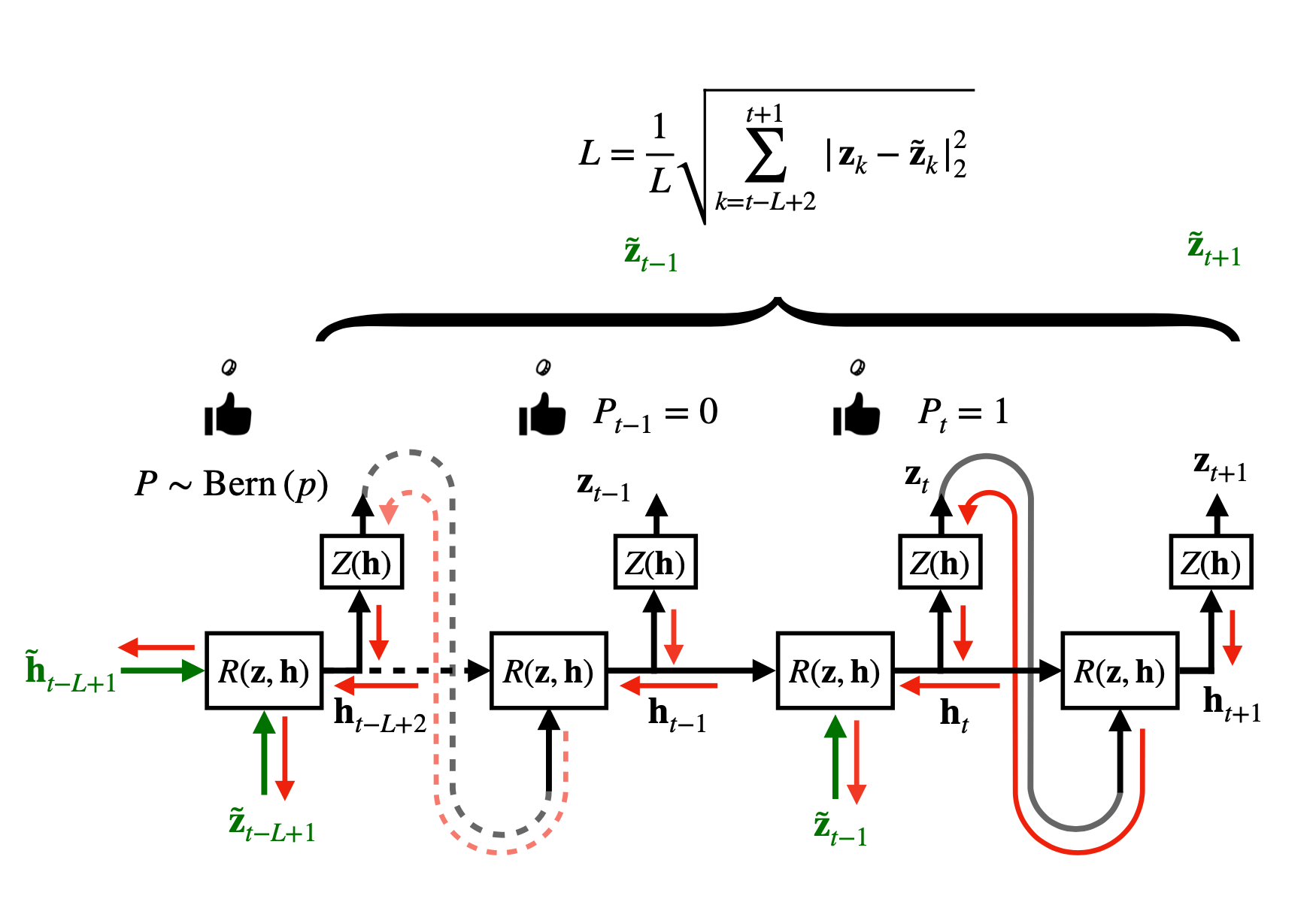Learning on predictions: Fusing training and autoregressive inference for long-term spatiotemporal forecasts

Pantelis R. Vlachas, and Petros Koumoutsakos

Journal of Nonlinear Dynamics, 2024

Abs arXiv Bib PDF

Recurrent Neural Networks (RNNs) have become an integral part of modeling and forecasting frameworks in areas like natural language processing and high-dimensional dynamical systems such as turbulent fluid flows. To improve the accuracy of predictions, RNNs are trained using the Backpropagation Through Time (BPTT) method to minimize prediction loss. During testing, RNNs are often used in autoregressive scenarios where the output of the network is fed back into the input. However, this can lead to the exposure bias effect, as the network was trained to receive ground-truth data instead of its own predictions. This mismatch between training and testing is compounded when the state distributions are different, and the train and test losses are measured. To address this, previous studies have proposed solutions for language processing networks with probabilistic predictions. Building on these advances, we propose the Scheduled Autoregressive BPTT (BPTT-SA) algorithm for predicting complex systems. Our results show that BPTT-SA effectively reduces iterative error propagation in Convolutional RNNs and Convolutional Autoencoder RNNs, and demonstrate its capabilities in long-term prediction of high-dimensional fluid flows.
@article{vlachas2024learning, doi = {10.1016/j.physd.2024.134371}, title = {Learning on predictions: Fusing training and autoregressive inference for long-term spatiotemporal forecasts}, author = {Vlachas, Pantelis R. and Koumoutsakos, Petros}, journal = {Journal of Nonlinear Dynamics}, year = {2024} }

2023

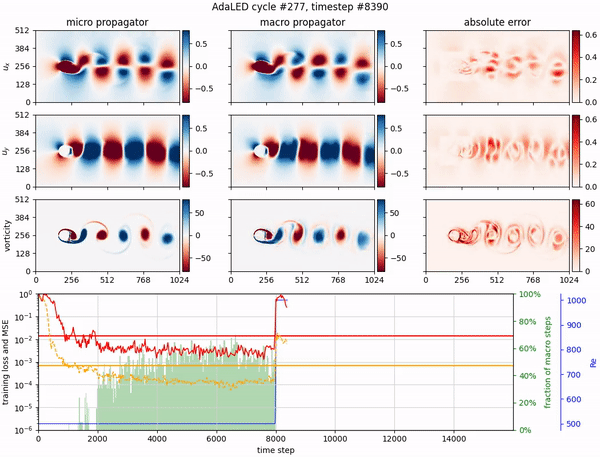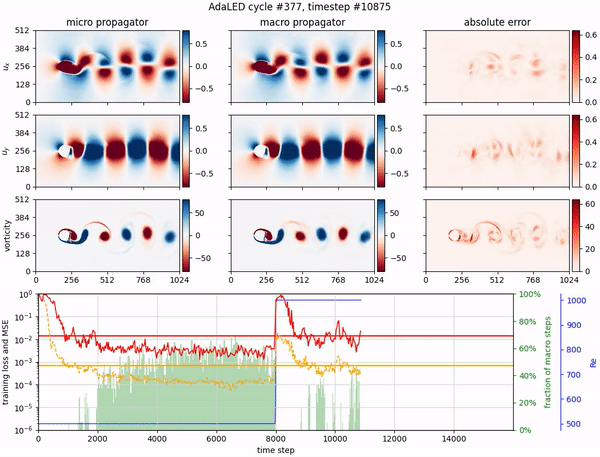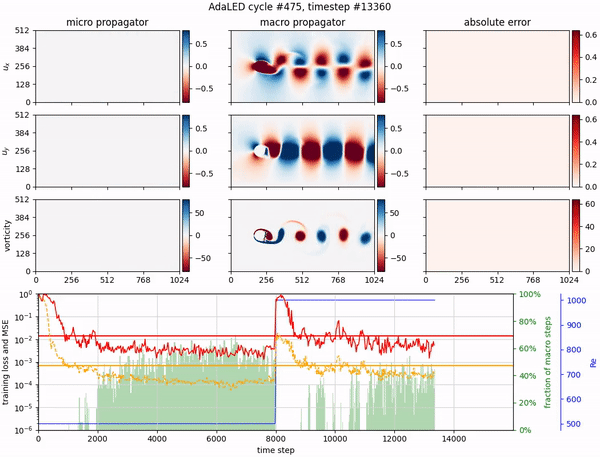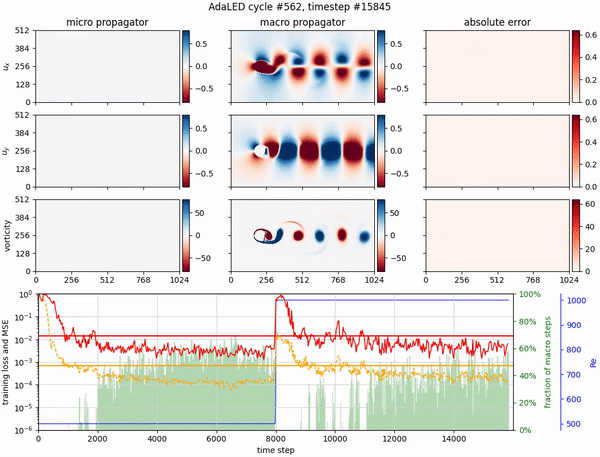Adaptive learning of effective dynamics for online modeling of complex systems

Ivica Kičić, Pantelis R. Vlachas, Georgios Arampatzis, Michail Chatzimanolakis, Leonidas Guibas, and Petros Koumoutsakos

Computer Methods in Applied Mechanics and Engineering, 2023

Abs arXiv Bib HTML PDF Code

Predictive simulations are essential for applications ranging from weather forecasting to material design. The veracity of these simulations hinges on their capacity to capture the effective system dynamics. Massively parallel simulations predict the systems dynamics by resolving all spatiotemporal scales, often at a cost that prevents experimentation. On the other hand, reduced order models are fast but often limited by the linearization of the system dynamics and the adopted heuristic closures. We propose a novel systematic framework that bridges large scale simulations and reduced order models to extract and forecast adaptively the effective dynamics (AdaLED) of multiscale systems. AdaLED employs an autoencoder to identify reduced-order representations of the system dynamics and an ensemble of probabilistic recurrent neural networks (RNNs) as the latent time-stepper. The framework alternates between the computational solver and the surrogate, accelerating learned dynamics while leaving yet-to-be-learned dynamics regimes to the original solver. AdaLED continuously adapts the surrogate to the new dynamics through online training. The transitions between the surrogate and the computational solver are determined by monitoring the prediction accuracy and uncertainty of the surrogate. The effectiveness of AdaLED is demonstrated on three different systems - a Van der Pol oscillator, a 2D reaction-diffusion equation, and a 2D Navier-Stokes flow past a cylinder for varying Reynolds numbers (400 up to 1200), showcasing its ability to learn effective dynamics online, detect unseen dynamics regimes, and provide net speed-ups. To the best of our knowledge, AdaLED is the first framework that couples a surrogate model with a computational solver to achieve online adaptive learning of effective dynamics. It constitutes a potent tool for applications requiring many expensive simulations.
@article{kivcic2023adaptive, doi = {10.1016/j.cma.2023.116204}, title = {Adaptive learning of effective dynamics for online modeling of complex systems}, author = {Ki{\v{c}}i{\'c}, Ivica and Vlachas, Pantelis R. and Arampatzis, Georgios and Chatzimanolakis, Michail and Guibas, Leonidas and Koumoutsakos, Petros}, journal = {Computer Methods in Applied Mechanics and Engineering}, volume = {415}, pages = {116204}, year = {2023}, publisher = {Elsevier} }

2022

Learning and forecasting the effective dynamics of complex systems across scales

Pantelis R. Vlachas

ETH Zurich, 2022

Abs Bib HTML PDF Slides

Simulations of complex systems are essential for applications ranging from weather forecasting to molecular systems and drug design. The veracity of the resulting predictions hinges on their capacity to capture the un- derlying system dynamics. Massively parallel simulations performed in High-Performance Computing (HPC) clusters capture these dynamics by resolving all spatio-temporal scales. The computational cost is often pro- hibitive for experimentation or optimization, while their findings might not allow for generalization. The design of dimensionality reduction methods and fast data-driven reduced-order models or surrogates have been matters of life-long research efforts. In the first part of this thesis, we focus on the design and training of data-driven recurrent neural networks for forecasting the spatio-temporal dynamics of high-dimensional and reduced-order complex systems. We propose architectural advances and training algorithms that alleviate the pitfalls of previously proposed methods, whose application was limited to lower-order systems. The designed algorithms extend the arsenal of predictive models for complex systems and spatio-temporal chaos. In the second part, we present a novel systematic framework that bridges large-scale simulations and reduced-order models to Learn the Effective Dynamics (LED) of complex systems. The framework forms algorithmic alloys between non-linear machine learning algorithms and the Equation- Free approach for modeling complex systems exhibiting spatio-temporal chaos. LED deploys autoencoders to map between fine- and coarse-grained representations and evolves the latent space dynamics using recurrent neural networks. The algorithm is validated on benchmark problems, and we find that it outperforms state-of-the-art reduced-order models in terms of predictability and large-scale simulations in terms of cost. LED is applicable to systems ranging from chemistry to fluid mechanics and reduces the computational effort by up to two orders of magnitude while maintaining the prediction accuracy of the full system dynamics. We argue that LED constitutes a potent novel modality for the accurate prediction of complex systems
@phdthesis{vlachas2022learning, doi = {10.3929/ethz-b-000551130}, title = {Learning and forecasting the effective dynamics of complex systems across scales}, author = {Vlachas, Pantelis R.}, year = {2022}, school = {ETH Zurich} }
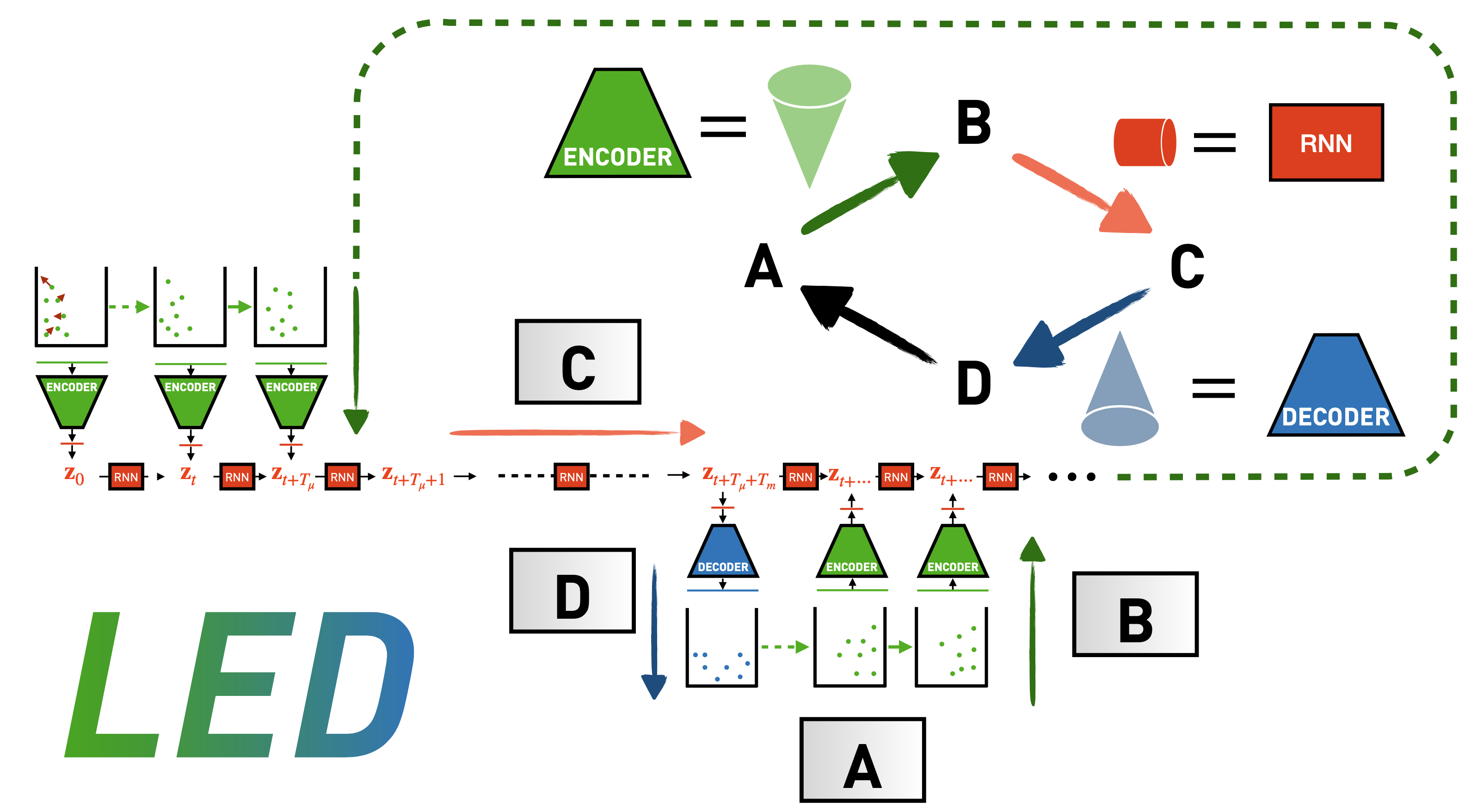Multiscale simulations of complex systems by learning their effective dynamics

Pantelis R. Vlachas, Georgios Arampatzis, Caroline Uhler, and Petros Koumoutsakos

Nature Machine Intelligence, 2022

Abs arXiv Bib HTML PDF Code

Predictive simulations of complex systems are essential for applications ranging from weather forecasting to drug design. The veracity of these predictions hinges on their capacity to capture effective system dynamics. Massively parallel simulations predict the system dynamics by resolving all spatiotemporal scales, often at a cost that prevents experimentation, while their findings may not allow for generalization. On the other hand, reduced-order models are fast but limited by the frequently adopted linearization of the system dynamics and the utilization of heuristic closures. Here we present a novel systematic framework that bridges large-scale simulations and reduced-order models to learn the effective dynamics of diverse, complex systems. The framework forms algorithmic alloys between nonlinear machine learning algorithms and the equation-free approach for modelling complex systems. Learning the effective dynamics deploys autoencoders to formulate a mapping between fine- and coarse-grained representations and evolves the latent space dynamics using recurrent neural networks. The algorithm is validated on benchmark problems, and we find that it outperforms state-of-the-art reduced-order models in terms of predictability, and large-scale simulations in terms of cost. Learning the effective dynamics is applicable to systems ranging from chemistry to fluid mechanics and reduces the computational effort by up to two orders of magnitude while maintaining the prediction accuracy of the full system dynamics. We argue that learning the effective dynamics provides a potent novel modality for accurately predicting complex systems.
@article{vlachas2022multiscale, title = {Multiscale simulations of complex systems by learning their effective dynamics}, author = {Vlachas, Pantelis R. and Arampatzis, Georgios and Uhler, Caroline and Koumoutsakos, Petros}, journal = {Nature Machine Intelligence}, volume = {4}, number = {4}, pages = {359--366}, year = {2022}, doi = {10.1038/s42256-022-00464-w}, publisher = {Nature Publishing Group UK London} }

2021

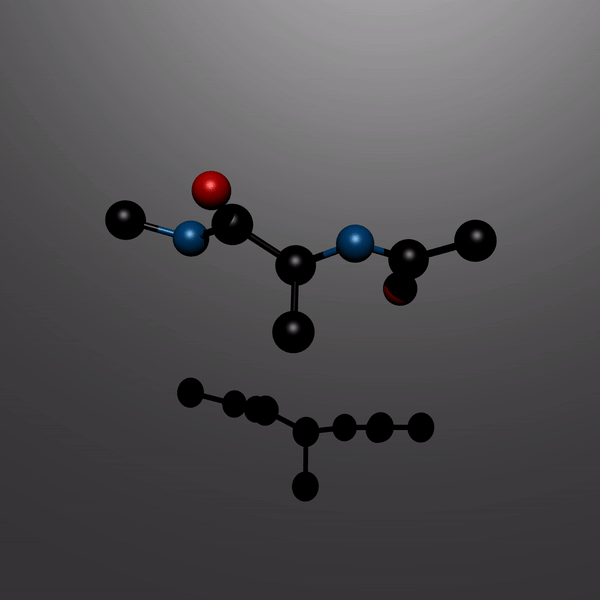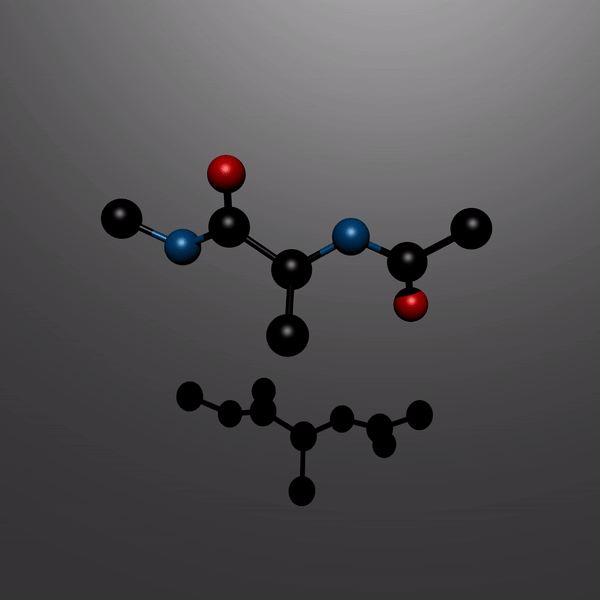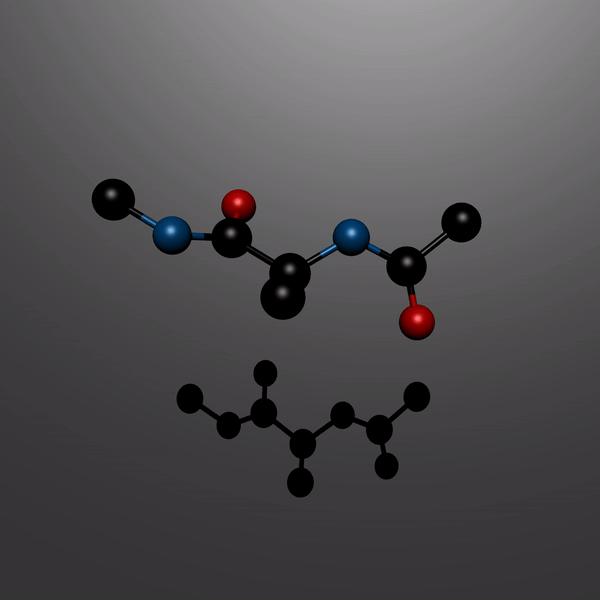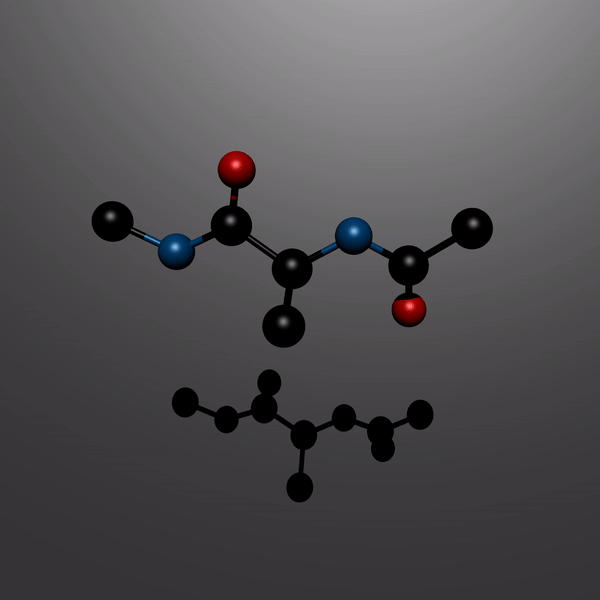Accelerated simulations of molecular systems through learning of effective dynamics

Pantelis R. Vlachas, Julija Zavadlav, Matej Praprotnik, and Petros Koumoutsakos

Journal of Chemical Theory and Computation, 2021

Abs arXiv Bib HTML PDF Code

Simulations are vital for understanding and predicting the evolution of complex molecular systems. However, despite advances in algorithms and special purpose hardware, accessing the time scales necessary to capture the structural evolution of biomolecules remains a daunting task. In this work, we present a novel framework to advance simulation time scales by up to 3 orders of magnitude by learning the effective dynamics (LED) of molecular systems. LED augments the equation-free methodology by employing a probabilistic mapping between coarse and fine scales using mixture density network (MDN) autoencoders and evolves the non-Markovian latent dynamics using long short-term memory MDNs. We demonstrate the effectiveness of LED in the Müller–Brown potential, the Trp cage protein, and the alanine dipeptide. LED identifies explainable reduced-order representations, i.e., collective variables, and can generate, at any instant, all-atom molecular trajectories consistent with the collective variables. We believe that the proposed framework provides a dramatic increase to simulation capabilities and opens new horizons for the effective modeling of complex molecular systems.
@article{vlachas2021accelerated, title = {Accelerated simulations of molecular systems through learning of effective dynamics}, author = {Vlachas, Pantelis R. and Zavadlav, Julija and Praprotnik, Matej and Koumoutsakos, Petros}, journal = {Journal of Chemical Theory and Computation}, volume = {18}, number = {1}, pages = {538--549}, year = {2021}, doi = {10.1021/acs.jctc.1c00809}, publisher = {ACS Publications} }

2020

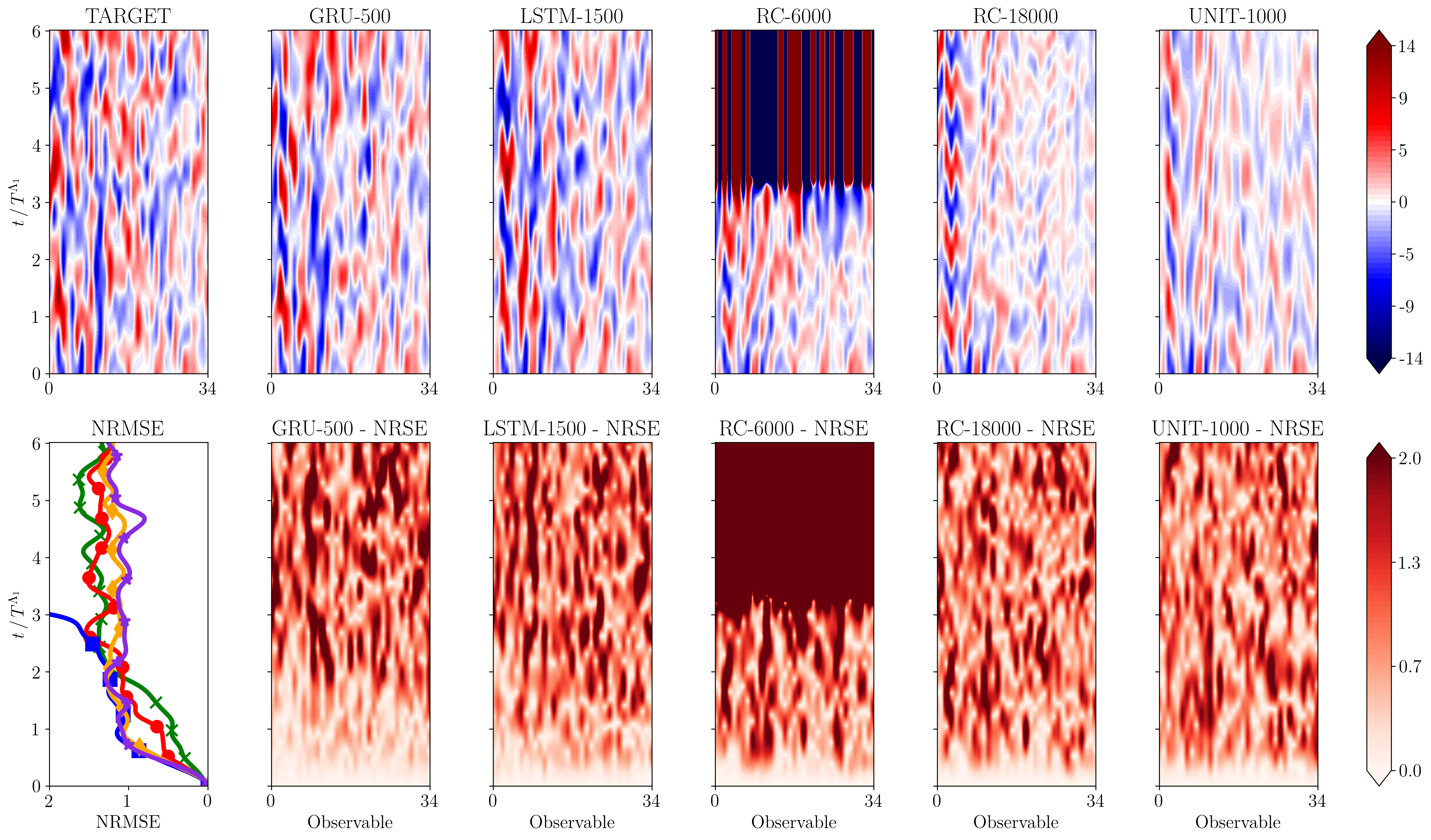Backpropagation algorithms and reservoir computing in recurrent neural networks for the forecasting of complex spatiotemporal dynamics

Pantelis R. Vlachas, Jaideep Pathak, Brian R Hunt, Themistoklis P Sapsis, Michelle Girvan, Edward Ott, and 1 more author

Neural Networks, 2020

Abs arXiv Bib HTML PDF Code

We examine the efficiency of Recurrent Neural Networks in forecasting the spatiotemporal dynamics of high dimensional and reduced order complex systems using Reservoir Computing (RC) and Backpropagation through time (BPTT) for gated network architectures. We highlight advantages and limitations of each method and discuss their implementation for parallel computing architectures. We quantify the relative prediction accuracy of these algorithms for the long-term forecasting of chaotic systems using as benchmarks the Lorenz-96 and the Kuramoto–Sivashinsky (KS) equations. We find that, when the full state dynamics are available for training, RC outperforms BPTT approaches in terms of predictive performance and in capturing of the long-term statistics, while at the same time requiring much less training time. However, in the case of reduced order data, large scale RC models can be unstable and more likely than the BPTT algorithms to diverge. In contrast, RNNs trained via BPTT show superior forecasting abilities and capture well the dynamics of reduced order systems. Furthermore, the present study quantifies for the first time the Lyapunov Spectrum of the KS equation with BPTT, achieving similar accuracy as RC. This study establishes that RNNs are a potent computational framework for the learning and forecasting of complex spatiotemporal systems.
@article{vlachas2020backpropagation, title = {Backpropagation algorithms and reservoir computing in recurrent neural networks for the forecasting of complex spatiotemporal dynamics}, author = {Vlachas, Pantelis R. and Pathak, Jaideep and Hunt, Brian R and Sapsis, Themistoklis P and Girvan, Michelle and Ott, Edward and Koumoutsakos, Petros}, journal = {Neural Networks}, volume = {126}, pages = {191--217}, year = {2020}, doi = {10.1016/j.neunet.2020.02.016}, publisher = {Elsevier} }
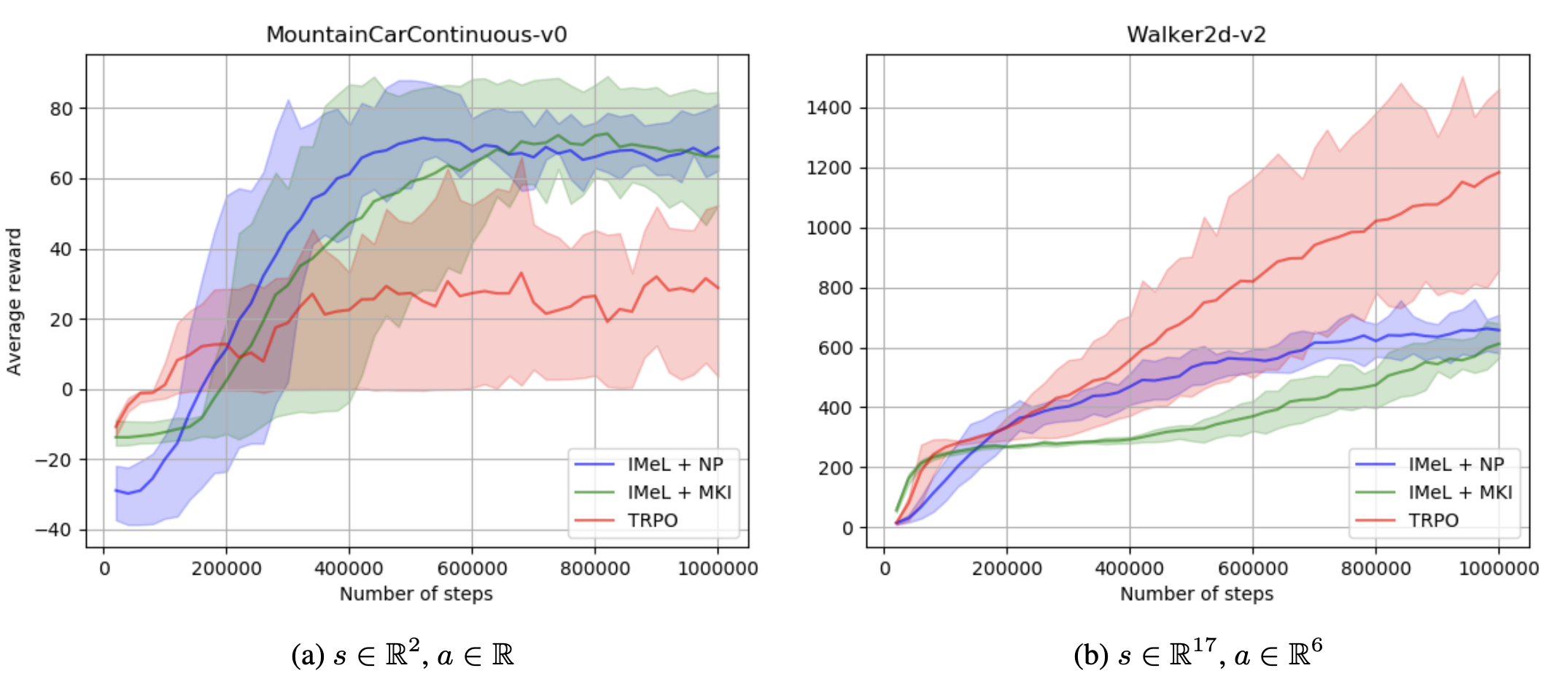Improved Memories Learning

Francesco Varoli, Guido Novati, Pantelis R. Vlachas, and Petros Koumoutsakos

arXiv preprint arXiv:2008.10433, 2020

Abs arXiv Bib PDF

We propose Improved Memories Learning (IMeL), a novel algorithm that turns reinforcement learning (RL) into a supervised learning (SL) problem and delimits the role of neural networks (NN) to interpolation. IMeL consists of two components. The first is a reservoir of experiences. Each experience is updated based on a non-parametric procedural improvement of the policy, computed as a bounded one-sample Monte Carlo estimate. The second is a NN regressor, which receives as input improved experiences from the reservoir (context points) and computes the policy by interpolation. The NN learns to measure the similarity between states in order to compute long-term forecasts by averaging experiences, rather than by encoding the problem structure in the NN parameters. We present preliminary results and propose IMeL as a baseline method for assessing the merits of more complex models and inductive biases.
@article{varoli2020improved, title = {Improved Memories Learning}, author = {Varoli, Francesco and Novati, Guido and Vlachas, Pantelis R. and Koumoutsakos, Petros}, journal = {arXiv preprint arXiv:2008.10433}, year = {2020} }

2018

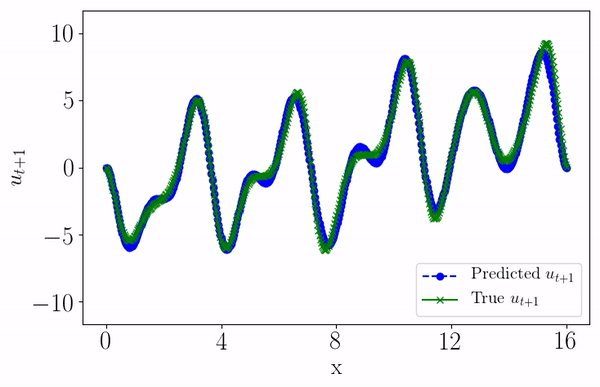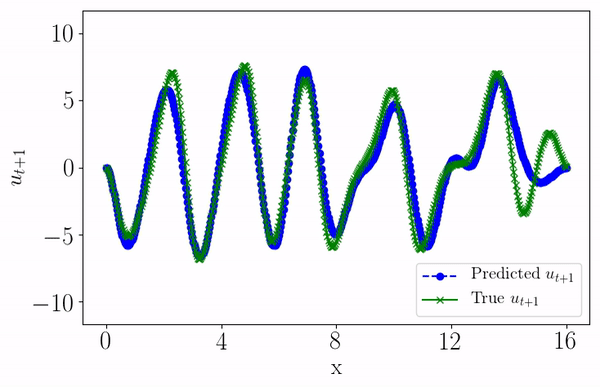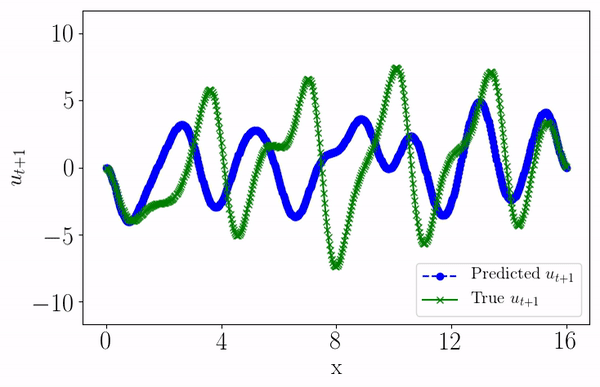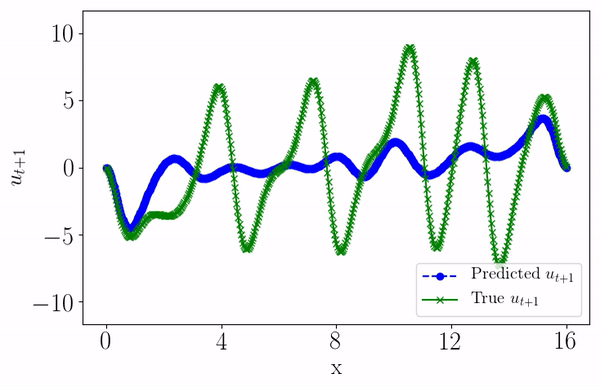Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks

Pantelis R. Vlachas, Wonmin Byeon, Zhong Y Wan, Themistoklis P Sapsis, and Petros Koumoutsakos

Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2018

Abs arXiv Bib HTML PDF Code

We introduce a data-driven forecasting method for high-dimensional chaotic systems using long short-term memory (LSTM) recurrent neural networks. The proposed LSTM neural networks perform inference of high-dimensional dynamical systems in their reduced order space and are shown to be an effective set of nonlinear approximators of their attractor. We demonstrate the forecasting performance of the LSTM and compare it with Gaussian processes (GPs) in time series obtained from the Lorenz 96 system, the Kuramoto–Sivashinsky equation and a prototype climate model. The LSTM networks outperform the GPs in short-term forecasting accuracy in all applications considered. A hybrid architecture, extending the LSTM with a mean stochastic model (MSM–LSTM), is proposed to ensure convergence to the invariant measure. This novel hybrid method is fully data-driven and extends the forecasting capabilities of LSTM networks.
@article{vlachas2018data, title = {Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks}, author = {Vlachas, Pantelis R. and Byeon, Wonmin and Wan, Zhong Y and Sapsis, Themistoklis P and Koumoutsakos, Petros}, journal = {Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences}, volume = {474}, number = {2213}, pages = {20170844}, year = {2018}, doi = {10.1098/rspa.2017.0844}, publisher = {The Royal Society Publishing} }
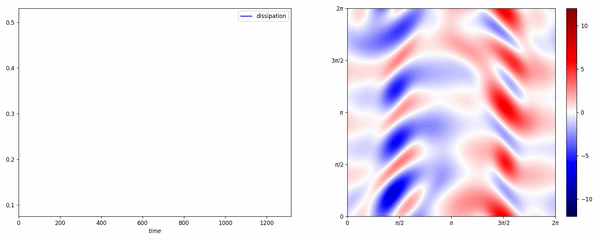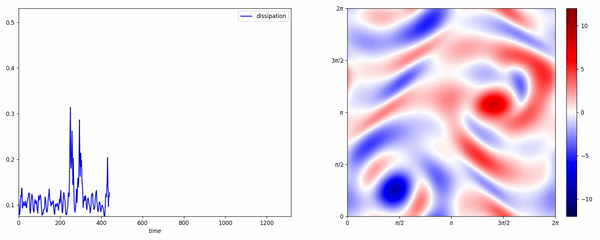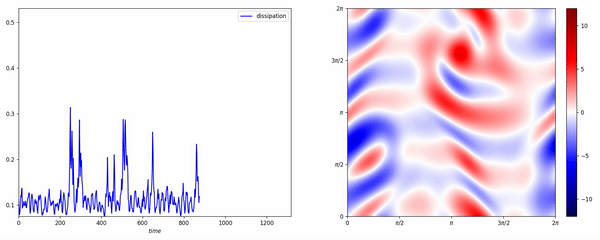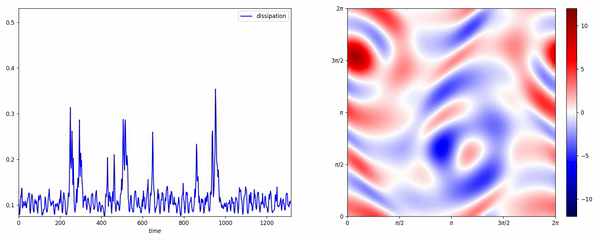Data-assisted reduced-order modeling of extreme events in complex dynamical systems

Zhong Yi Wan, Pantelis R. Vlachas, Petros Koumoutsakos, and Themistoklis Sapsis

PloS one, 2018

Abs arXiv Bib HTML PDF Code

The prediction of extreme events, from avalanches and droughts to tsunamis and epidemics, depends on the formulation and analysis of relevant, complex dynamical systems. Such dynamical systems are characterized by high intrinsic dimensionality with extreme events having the form of rare transitions that are several standard deviations away from the mean. Such systems are not amenable to classical order-reduction methods through projection of the governing equations due to the large intrinsic dimensionality of the underlying attractor as well as the complexity of the transient events. Alternatively, data-driven techniques aim to quantify the dynamics of specific, critical modes by utilizing data-streams and by expanding the dimensionality of the reduced-order model using delayed coordinates. In turn, these methods have major limitations in regions of the phase space with sparse data, which is the case for extreme events. In this work, we develop a novel hybrid framework that complements an imperfect reduced order model, with data-streams that are integrated though a recurrent neural network (RNN) architecture. The reduced order model has the form of projected equations into a low-dimensional subspace that still contains important dynamical information about the system and it is expanded by a long short-term memory (LSTM) regularization. The LSTM-RNN is trained by analyzing the mismatch between the imperfect model and the data-streams, projected to the reduced-order space. The data-driven model assists the imperfect model in regions where data is available, while for locations where data is sparse the imperfect model still provides a baseline for the prediction of the system state. We assess the developed framework on two challenging prototype systems exhibiting extreme events. We show that the blended approach has improved performance compared with methods that use either data streams or the imperfect model alone. Notably the improvement is more significant in regions associated with extreme events, where data is sparse.
@article{wan2018data, title = {Data-assisted reduced-order modeling of extreme events in complex dynamical systems}, author = {Wan, Zhong Yi and Vlachas, Pantelis R. and Koumoutsakos, Petros and Sapsis, Themistoklis}, journal = {PloS one}, volume = {13}, number = {5}, pages = {e0197704}, year = {2018}, doi = {10.1371/journal.pone.0197704}, publisher = {Public Library of Science San Francisco, CA USA} }

2015

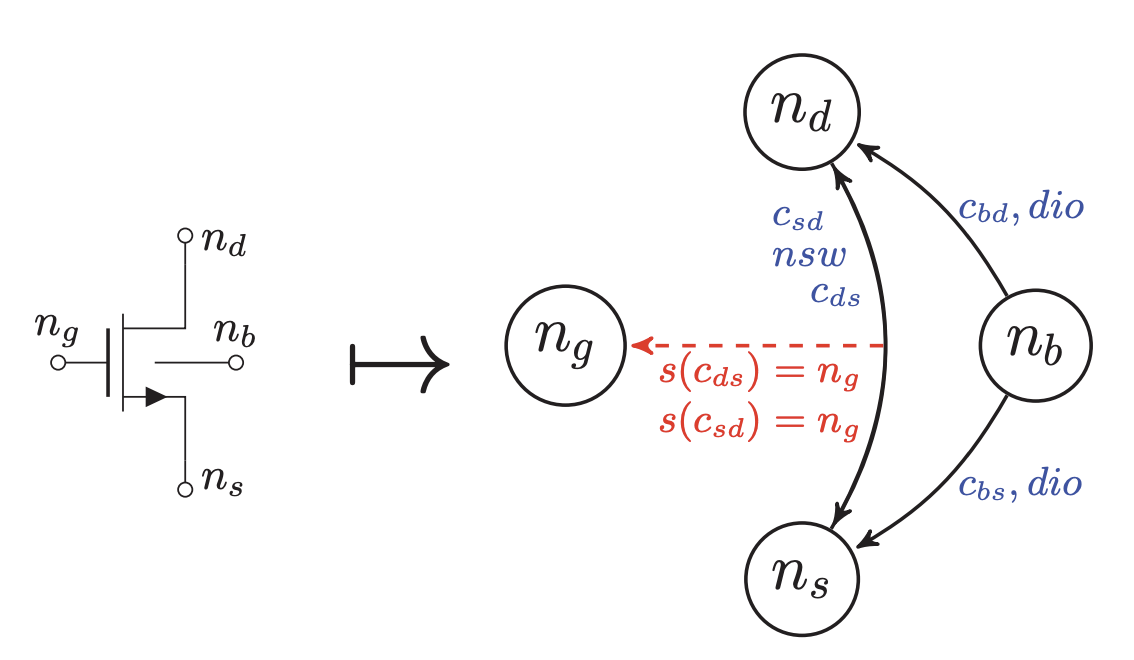A fast analytical approach for static power-down mode analysis

Michael Zwerger, Pantelis R. Vlachas, and Helmut Graeb

In 2015 IEEE International Conference on Electronics, Circuits, and Systems (ICECS), 2015

Abs Bib HTML PDF

In this paper, a new method for static analysis of the power-down mode of analog circuits is presented. Floating nodes are detected. The static node voltages are estimated. It can be verified that no current is flowing. The method is based on circuit structure. No numerical simulation is needed. The presented approach solves an integer constraint program. Experimental results show a speed-up of factor 2.5 compared a state-of-theart voltage propagation algorithm. Furthermore, the presented analytical problem formulation enables fast implementation of the method using a constraint programming solver.
@inproceedings{zwerger2015fast, title = {A fast analytical approach for static power-down mode analysis}, author = {Zwerger, Michael and Vlachas, Pantelis R. and Graeb, Helmut}, booktitle = {2015 IEEE International Conference on Electronics, Circuits, and Systems (ICECS)}, pages = {1--4}, year = {2015}, doi = {10.1109/ICECS.2015.7440234}, organization = {IEEE} }